De optiegrieken: delta, gamma, vega en theta

Helaas behoren de optiegrieken niet tot de meest spannende materie om te bespreken, maar het is voor het kopen en verkopen van opties wel van groot belang om de theorie achter de optiegrieken goed te begrijpen.

De optiegrieken delta, gamma, vega en theta geven beleggers inzicht in de prijsvorming van opties en zijn daarmee van cruciaal belang voor een optiehandelaar. Zo wordt een optiepremie onder andere bepaald door de koers van de onderliggende waarde, de looptijd van de optie tot expiratie en de volatiliteit.

In dit artikel leggen we u meer uit over de vier optiegrieken en bespreken we stap voor stap waar u rekening mee dient te houden bij het handelen in opties.

Bent u op zoek naar een broker om opties te handelen, klik dan hier.

De optiegrieken

Deze koers van de onderliggende waarde, de looptijd van de optie tot expiratie en de volatiliteit zijn geen constante variabelen. Zo kan de volatiliteit bijvoorbeeld toenemen wanneer de onzekerheid toeneemt, met als gevolg een stijging van de optiepremie.

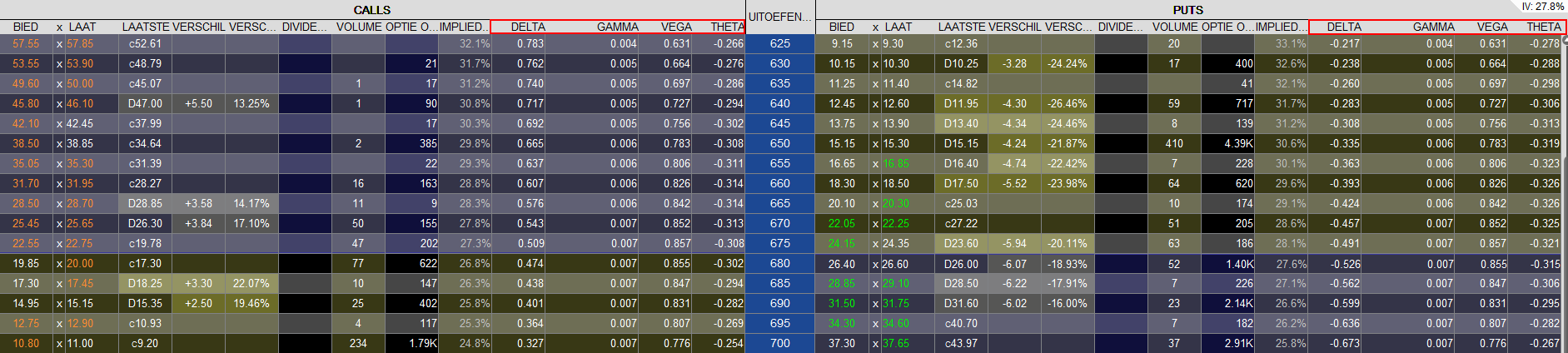
De optiegrieken geven een handelaar inzicht in de prijsverandering van een optiepremie wanneer de variabelen veranderen. De onderstaande afbeelding van de Optie Trader laat zien hoe u binnen het TWS Handelsplatform de optiegrieken inzichtelijk krijgt.

Optiegriek 1: Delta

De delta is de belangrijkste optiegriek en heeft betrekking op de verandering in de prijs van een optie in verhouding tot een verandering in de prijs van de onderliggende waarde. De delta geeft dus weer in welke mate de optiepremie fluctueert bij een koersstijging of –daling van het onderliggende aandeel. Met een beweging in de onderliggende waarde wordt standaard uitgegaan van een stijging of daling van de prijs met 1 punt.

In het bovenstaande theoretische voorbeeld heeft een calloptie een premie van € 2,50 en bedraagt de delta 0.5. Wanneer de onderliggende waarde stijgt met € 1, dan neemt de waarde van de optie toe met € 0,50 tot € 3,00.

Premie calloptie € 2,50 ➔ Delta 0.50 ➔ Premie calloptie € 3,00

Andersom werkt het op dezelfde manier. Daalt de onderliggende waarde met € 1, dan neemt de optiepremie af met € 0,50 en zakt deze naar € 2.

Premie calloptie € 2,50 ➔ Delta 0.50 ➔ Premie calloptie € 2,00

De werking van de delta voor putopties is identiek, behalve dat de putdelta met een – (min teken) wordt getoond. Daalt de onderliggende waarde met 1 punt, dan neemt de premie van de putoptie toe met de delta. Stijgt de onderliggende waarde met 1 punt, dan neemt de premie van de putoptie af met de delta.

Overigens heeft de delta nog een tweede definitie. De delta geeft namelijk ook weer wat de kans is dat een optie in-the-money expireert. Dit is geen wetenschappelijke benadering, maar een rule of thumb. Een optiehandelaar is op deze manier in staat om snel in te schatten of een optie een grote of kleine kans heeft om in-the-money te expireren.

Stel dat de delta van een optie 0.80 bedraagt, dan is de kans 80% dat de optie op afloopdatum in-the-money expireert. Heeft een optie een delta van 0.10, dan is deze kans slechts 10%. Een at-the-money optie heeft daarom delta 0.50, waarmee de kans dus 50% is dat deze in-the-money expireert.

Optiegriek 2: Gamma

Wanneer de onderliggende waarde van een optie beweegt, wordt een optie meer in-the-money of meer out-of-the-money. Dit heeft tot gevolg dat ook de delta constant verandert. Deze verandering van de delta wordt gemeten aan de hand van de optiegriek gamma. De gamma geeft de wijziging in de waarde van de delta weer wanneer de onderliggende waarde beweegt. De gamma is het grootst bij at-the-money opties, aangezien beweging in de onderliggende waarde dan de meeste invloed heeft op de delta van deze opties.

In de onderstaande tabel worden de delta en gamma voor callopties op AEX getoond die een looptijd hebben van een maand. De AEX noteert in dit voorbeeld rond de 490 punten. De waardes van de gamma zijn afgerond om de materie eenvoudig over te kunnen brengen.

De at-the-money optie met uitoefenprijs 490 heeft de grootste gamma van 0.02. Stijgt de AEX met 1 punt, dan wijzigt de delta met 0.02. De berekening is eenvoudig: u telt de gamma bij de delta op wanneer de AEX met 1 punt stijgt of trekt deze er vanaf wanneer de AEX 1 punt daalt. De delta van de calloptie 490 wijzigt dus na 1 punt stijging van 0.51 naar 0.53.

Wanneer de opties een kortere looptijd hebben, wordt de gamma groter. De verklaring hiervoor is vrij simpel. Kortlopende opties hebben minder tijdswaarde dan langer lopende opties. Beweging in de onderliggende waarde is dus van grotere invloed op de optiepremie dan bij langer lopende opties. Wanneer u bijvoorbeeld de gamma opzoekt van een dag- of weekoptie, zult u zien dat deze vele malen groter zijn dan in het besproken voorbeeld.

Optiegriek 3: Vega

De derde optiegriek is de vega. Aangezien opties geprijsd worden aan de hand van de verwachte beweeglijkheid van het onderliggende effect, speelt volatiliteit een belangrijke rol. Voor het begrijpen van de vega is het noodzakelijk om te realiseren dat volatiliteit betrekking heeft op de te verwachten beweeglijkheid van de onderliggende waarde tot expiratiedatum. In optietermen wordt dit de implied volatiliteit genoemd.

De vega van een optie geeft weer in welke mate de prijs van een optie verandert als de volatiliteit wijzigt. Een afname van de volatiliteit zorgt ervoor dat er minder beweging wordt verwacht in de prijs van de onderliggende waarde, waardoor opties goedkoper worden. Bij een toename van de volatiliteit neemt de verwachte beweeglijkheid van de onderliggende waarde toe en worden opties juist duurder.

De vega verschilt per uitoefenprijs en de looptijd van een optie. Een kortlopende optie is minder gevoelig voor veranderingen in de volatiliteit dan een langer lopende optie. De vega wordt net als alle andere optiegrieken als decimaal genoteerd, welke betrekking heeft op één punt wijziging in de implied volatiliteit van de optie.

De onderstaande tabel toont de vega voor at-the-money opties op de AEX met verschillende looptijden.

De vega in absolute termen is altijd kleiner bij korter lopende opties dan bij langer lopende opties. Hierbij dient wel in acht genomen te worden dat juist bij deze korter lopende opties de wijzigingen in de implied volatiliteit sneller plaatsvinden.

De implied volatiliteit geeft namelijk weer wat de verwachte beweeglijkheid is van de optie tot expiratiedatum. Zonder te ver vooruit te lopen op de materie is het belangrijk om te realiseren dat volatiliteit continu wijzigt en dit heeft te maken met onder andere vraag en aanbod en marktverwachtingen. Wanneer de marktverwachtingen wijzigen door een plotselinge gebeurtenis, zal dit de grootste invloed hebben op kortlopende opties.

Dus ondanks dat de vega absoluut het kleinst is voor de opties met een looptijd van bijvoorbeeld 1 maand, zijn de fluctuaties in de implied volatiliteit het grootst.

Neemt de implied volatiliteit van een AEX calloptie 490 die over 32 dagen expireert toe van 17,77% naar 19,77%, dan stijgt de optie premie met € 1,16 (2 x 0.58). Anderzijds, neemt de volatiliteit af, dan daalt de waarde van de optie. Volatiliteit is daarmee een cruciaal begrip bij het handelen van opties.

Optiegriek 4: Theta

De vierde en laatste optiegriek die we bespreken is de theta. De theta heeft betrekking op de tijdswaarde van opties. Gekochte opties geven een optiebelegger het recht om tot de afloopdatum van de optie aandelen te kopen of te verkopen.

Wanneer bijvoorbeeld een out-of-the-money calloptie gekocht wordt, is de betaalde premie voor de optie niets anders dan de verwachtingswaarde. Out-of-the-money opties hebben immers geen intrinsieke waarde. Wanneer de optie op expiratiedatum geen intrinsieke waarde heeft, dan wordt deze niet uitgeoefend en loopt de optie waardeloos af.

Vanaf het moment van aankoop tot expiratiedatum loopt de tijdswaarde in het begin langzaam, maar steeds sneller, uit de optie. De theta geeft als optiegriek weer in welke mate de tijdswaarde per dag uit de optie loopt.

De theta geeft dus weer hoeveel tijdswaarde de optie per dag verliest. Hoe korter de looptijd van een optie, des te sneller verliest de optie haar tijdswaarde. Dit is gelukkig heel simpel te begrijpen. Bij twee opties met dezelfde uitoefenprijs maar verschillende expiratiedata, verliest de korter lopende optie meer tijdswaarde per dag dan de langer lopende optie. Vanaf ongeveer één maand voor expiratie loopt deze tijdswaarde exponentieel uit de optie.

De onderstaande tabel toont de theta van at-the-money AEX-opties waarbij de looptijd verschilt.

De optie die over één maand expireert, verliest ongeveer € 0,16 aan optiepremie per dag. Naarmate expiratie dichterbij komt, zal de theta toenemen. De optie die over bijna zeven maanden expireert verliest ‘slechts’ € 0,06 aan tijdswaarde per dag.

Overigens is het verlies aan tijdswaarde een constant proces. Het is dus niet zo dat het verlies aan tijdswaarde plaatsvindt vanaf het slot tot de opening op de volgende handelsdag. Gedurende de dag loopt de tijdswaarde zo goed als onzichtbaar uit de optie. Uiteraard is het verlies aan tijdswaarde in het weekend het grootst.

De theta hangt ook samen met de volatiliteit. Wanneer de volatiliteit van opties relatief hoog is, zal de optie meer aan tijdswaarde verliezen. De verwachte beweeglijkheid is dan namelijk hoger.

Zoals eerder aangegeven zal ik in het volgende blog het begrip volatiliteit in detail aan u toelichten, zodat we na deze ‘droge’ theorie een vervolgstap kunnen maken naar de verschillende optiestrategieën zoals de covered call/covered put, call en put spreads, straddle, strangle, butterfly en iron condor.

Optiegrieken gebruiken bij opties handelen via LYNX?

Via LYNX kunt u zeer voordelig beleggen in opties. Met één simpele muisklik handelt u eenvoudig in alle Europese en Amerikaanse aandelenopties en indexopties. Tevens heeft u de beschikking over de beste trader tools, zoals de OptieTrader en kunt u optiecombinaties in zijn geheel naar de beurs versturen.